알고리즘 자료 모음

어떤 수학적인 문제^problem를 유한한 단계 안에 해결하기 위한 방법 혹은 절차를 알고리즘^algorithm이라고 한다.

a finite set of instructions for solving a problem

복잡도

시간 복잡도^{time complexity}

어떤 결정형 문제가 주어졌을 때, 그것을 계산할 수 있는 알고리즘의 시간 복잡도에 따라 그 문제는 P 혹은 NP로 분류될 수 있다. ( P와 NP 둘 다 아닐 수도 있다.)

어떤 문제를 풀기위한 알고리즘의 최소시간 복잡도를 알 수 있을까?
알 수 있는 문제가 바로 P 이고, 알 수 없는 문제가 바로 NP이다.

결정형 문제

결정형 문제^{decision problem}란 그 답이 'yes’와 ‘no’ 둘 중의 하나로 결정되는 문제를 뜻한다.

P와 NP는 결정형 문제에 한해서 정의된다.
이와 대조되는 개념으로 답에 셋 이상의 경우의 수가 있는 문제를 함수형 문제^{function problem}라고 한다.

어떤 결정형 문제에 대해 유한한 시간 내에 답이 '예’인 경우와 '아니오’인 경우 모두를 답할 수 있으면 그 문제는 결정 가능하다^decidable라고 한다.

결정성 알고리즘

결정성 알고리즘^{deterministic algorithm}은 '각 단계에서 그 다음 단계가 유일하게 결정되는 알고리즘’을 말한다. 우리가 여러 프로그래밍 언어로 작성하는 코드는 모두 결정성 알고리즘에 의한 것이다.

비결정성 알고리즘

비결정성 알고리즘^{non-deterministic algorithm}은 '각 단계에서 그 다음 단계가 유일하게 결정되지 않는 알고리즘’을 말한다.

P

Polynomial
다항식 시간에 Yes 또는 No 대답을 할 수 있으면 P

P = set of decision problems that can be solved in polynomial step of the input bit size by a TM

P 문제 : (결정론적) 튜링 기계로 다항식 시간 내에 해결 가능한 문제
즉 빅오 표기법으로 표현하면 해결 시간이 다항식 꼴이 나오는 문제이다.

P 문제는 결정성 알고리즘으로 다항식 시간 내에 해결 가능한 결정형 문제이다.

P is similar to a problem that a normal people can find its solution easily.

P : 어떤 문제의 해답을 빠른 시간(=다항 함수)안에 찾을 수 있는 문제.

다항 함수 : 한 변수의 곱셉과 덧셈으로만 이루어진 식. (3+2x²+5x³)

NP

Nondeterministic Polynomial (Non-Polynomial의 준말이 아님!)
Yes 대답이 나오는 해를 제공했을 때, 이것이 Yes 대답을 내는 해라는 사실을 다항식 시간에 확인해줄 수 있으면 NP

NP = set of decision problems for which any yes instance has some 'proof' that verifies the problem to be yes in polynomial step
(다른정의: NP = set of decision problems that cat be solved in polynomial step by a Nondeterministic TM)

NP 문제 : (다항식 시간 안에 해결 가능한지는 모르겠지만, 입력한 답이 맞을 경우) 맞다는 것을 다항식 시간 내에 증명 가능한 문제.
이는 "'비결정론적 튜링 기계’로 다항식 시간 내에 해결 가능한 문제"라고도 한다.(무수히 많은 튜링 기계를 병렬로 묶은 다음 가능한 모든 경우를 넣으면 다항식 시간 후에 그 중 하나가 정답을 알아내게 되기 때문이다.)

NP 문제는 비결정성 알고리즘으로 다항식 시간 내에 해결 가능한 결정형 문제이다.

NP is a problem that a normal people can grade whether other person’s solution is correct or not easily.

NP : 어떤 문제에 대해 내가 제시한 답이 정답인지 아닌지만 빠른 시간안에 O, Xㄹ 판단 할 수 있는 문제. (따라서 정답을 찾는 데 매우 오랜 시간이 걸린다. 어떤 문제를 빠른 시간안에 풀 수 있는 알고리즘이 존재한다고 증명되기만해도 P문제에 속한다.)

결정성 알고리즘은 비결정성 알고리즘에서 비결정도가 1인 특수한 경우이다. 그러므로 P 클래스가 NP 클래스에 포함됨은 명백하다.

환원

환원^reduction이란 간단히 말해 한 문제를 이용하여 다른 문제를 푸는 것을 뜻한다.

Turing Machine

A Turing Machine TM is a device which manipulates symbols on an (infinite) tape according to a finite amount of manipulation rules.

NP-Hard

NP-난해(NP-hard) 문제는 쉽게 표현하면 '어려운 문제’로, 모든 경우의 수를 전부 확인하면서 해를 구하는 방법 이외에는 딱히 방법이 없는 문제를 가리킨다. Approximation이나 Heuristic한 방법으로 풀게 된다. TSP(외판원 문제, Traveling Salesman Problem)가 대표적인 NP-난해 문제이다.

NP-Hard : 모든 NP 문제들을 빠른 시간 안에 이 문제로 Reduction 이 가능할 때.
(Reduction은 문맥상의 의미만 간단히 말하면, A라는 문제를 B문제로 바꾸어서 풀 수 있다는 것이다. 참고로 이때 문제를 바꾸는데에는 다항함수 시간이 걸린다.)

NP-complete

NP-완전(NP-complete, NP-C) 문제 : 'NP 집합에 속하는 결정 문제 중에서 가장 어려운 문제의 부분집합’으로, NP와 NP-난해의 교집합이 NP-완전임이 알려져 있다. 모든 NP 문제를 다항 시간 내에 NP-완전 문제로 환산할 수 있으므로 NP-완전 문제 중 하나라도 P에 속한다는 것을 증명한다면 모든 NP 문제가 P에 속하기 때문에, P-NP 문제가 P=NP의 형태로 풀리게 된다. 반대로 NP-완전 문제 중의 하나가 P에 속하지 않는다는 것이 증명된다면 P=NP에 대한 반례가 되어 P-NP 문제는 P≠NP의 형태로 풀리게 된다.

NP-Complete : NP이면서 NP-Hard인 문제. 즉 모든 NP 문제들이 이 'NP문제’로 Reduction이 가능할 때.
(어떤 NP 문제가 다항함수 시간안에 NP-Complete으로 Reduction이 가능한 경우, 그 문제도 역시 NP-Complete임이 증명되어있다. 그래서 1개의 NP-Complete이 발견된 이후 많은 문제들이 그 문제를 통해 Reduction 되어 NP-Complete임을 증명했다.)

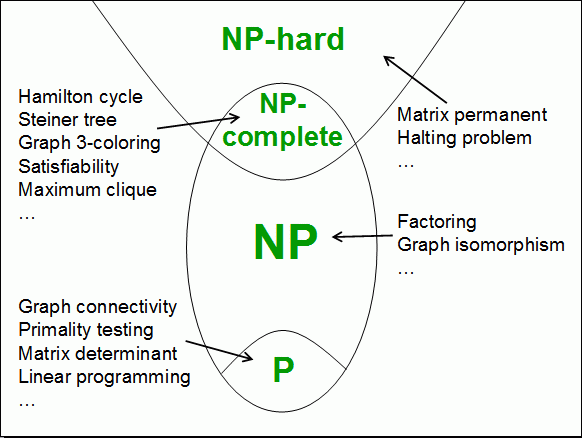
그 외

co-NP 문제 : (다항식 시간 안에 해결 가능한지는 모르겠지만, 입력한 답이 틀린 경우) 틀렸다는 것을 다항식 시간 내에 증명 가능한 문제.
P는 NP와 co-NP 모두의 부분집합이며, 둘 모두의 진부분집합일 것으로 추정된다고 한다. 소수 판정 문제가 co-NP로 분류된다고 한다.(아마 주어진 수가 소수가 아닌 경우엔 다항식 시간 안에 아님을 증명할 수 있기 때문인듯.{M. Agrawal의 PRIMES is in P (2004)에 따르면 소수 판정 문제는 P 문제라고 한다. 즉 당연히 co-NP이면서 NP이기까지도 한 것.})

해밀턴 경로 문제는 NP 문제이다. "그래프상의 모든 점을 한번씩만 지나가는 경로가 존재하는가?"의 답이 Yes이고 그 경로가 있을 경우 확인 자체는 가능하기 때문이다. 하지만 여기서 '존재하지 않는다’를 증명하는 것은 어렵고(일반해가 없다고 한다.), 따라서 co-NP 문제는 아니게 된다.

TSP는 엄밀하게, "변마다 가중치가 주어진 완전 그래프(weighted complete graph)에서 가장 적은 비용(cost)이 드는 해밀톤 회로(Hamiltonian cycle)을 구하는 것"이다. TSP의 형식을 yes/no가 되도록 "x 값이 주어졌을 때 x보다 비용이 적게 드는 회로가 있는가"로 표현하면 NP 문제 또한 되므로 NP-완전 문제가 된다. 일반적인 TSP에 대한 근사 알고리즘(Approximation algorithm)은 P=NP가 아니면 존재하지 않는다고 한다.(근사조차 존재하지 않다니!)

SAT(boolean SATisfiability problem)는 대표적인 NP-완전 문제로, $\sim, \land, \lor$ 세 논리 연산자와 여러 논리 변수의 결합으로 표현된 논리식이 주어졌을 때 그 식이 참이 되는 변수값이 존재하는지를 찾는 문제이다. 해가 주어졌을 때 다항식 시간 동안 옳은 지를 판별할 수 있으며(NP), 딱히 알고리즘이 주어지지 않았다고 한다(NP-난해).

정지 문제(halting problem)는 프로그램과 입력값이 주어졌을 경우 이 프로그램이 멈출 지 계속 돌아갈 지를 결정할수 있는가를 묻는 문제로, 대표적인 NP-난해 문제이다. 이는 입력이 참일 때만 멈추고 거짓일 때는 무한루프를 도는 SAT를 통해 NP-난해함을 볼 수 있고, 무한루프를 돌기 때문에 NP는 아니게 된다.

P=NP 문제는 수학 및 전산학의 미해결 문제 중 하나로, P와 NP가 같은 집합인지 아닌지(아니라면 진부분집합이 된다)를 묻는 문제이다. 7개의 밀레니엄 문제 중 하나이다. 한편 NP=co-NP 문제는 P=NP문제 만큼이나 어렵고 중요한 문제이나, 그만큼의 집중은 받지 못하고 있다고 한다.

참고

저작자표시 비영리 변경금지

Beyond Cool, Adventure Forever!

알고리즘 용어